Đố bạn tìm được lỗi sai trong phép toán chứng minh 90 = 100

Cho tứ giác ABCD, trong đó, cạnh AD = BC = x, góc A vuông và góc B là 100°.

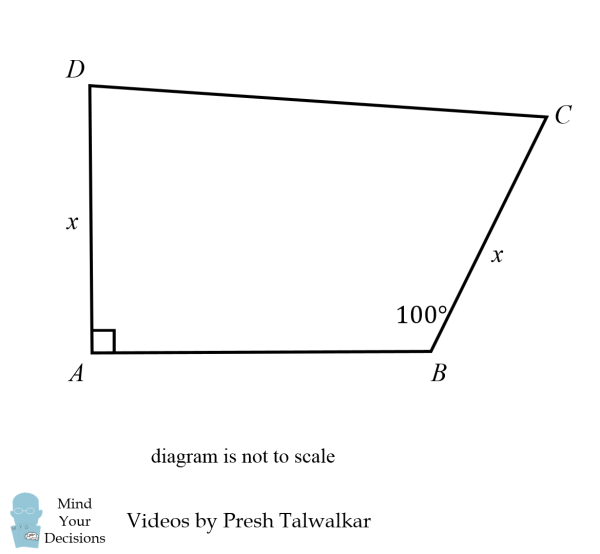
Kẻ đường trung trực của CD và AB. Gọi giao điểm của 2 đường thẳng là E.

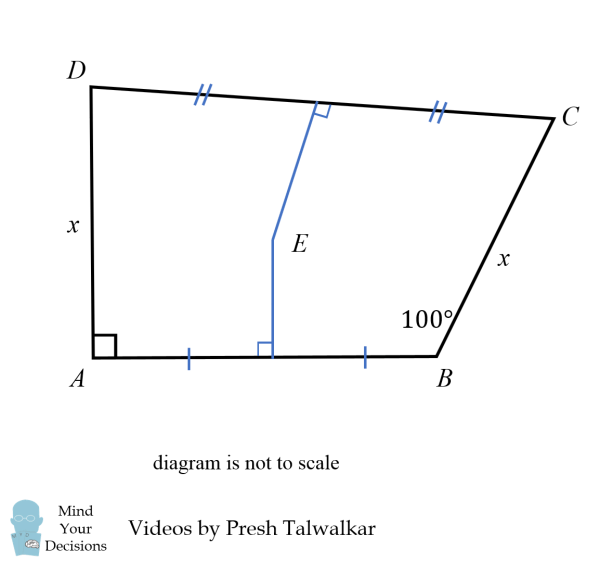
Vì E nằm trên đường đường trung trực của AB, nên AE = BE = y (2 cạnh huyền của 2 tam giác vuông có 1 cạnh góc vuông chung, 1 cạnh góc vuông bằng nhau). Tương tự, DE = CE = z.

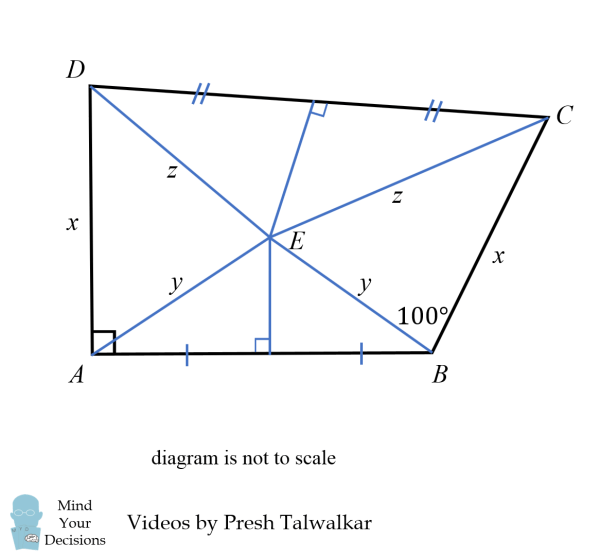
Xét tam giác AED và tam giác BEC. Vì chúng có 3 cạnh tương ứng bằng nhau nên 2 tam giác này đồng dạng. Do đó góc CBE = góc DAE = α.

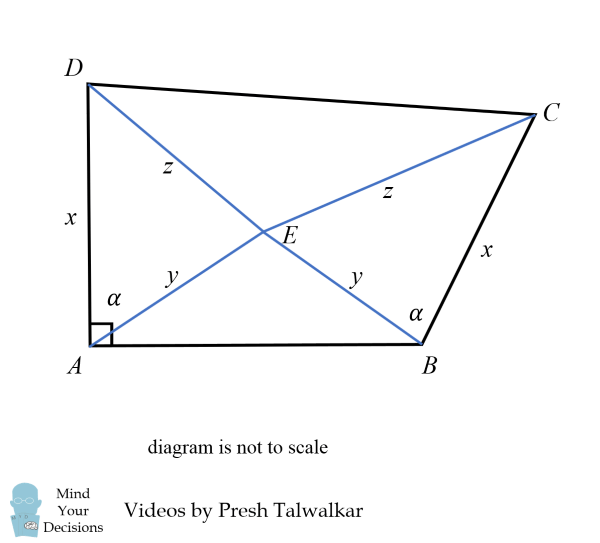
Xét tam giác FAE và tam giác FBE. Vì chúng cũng có 3 cạnh tương ứng bằng nhau nên 2 tam giác này đồng dạng. Do đó, góc FAE = góc FBE = β.

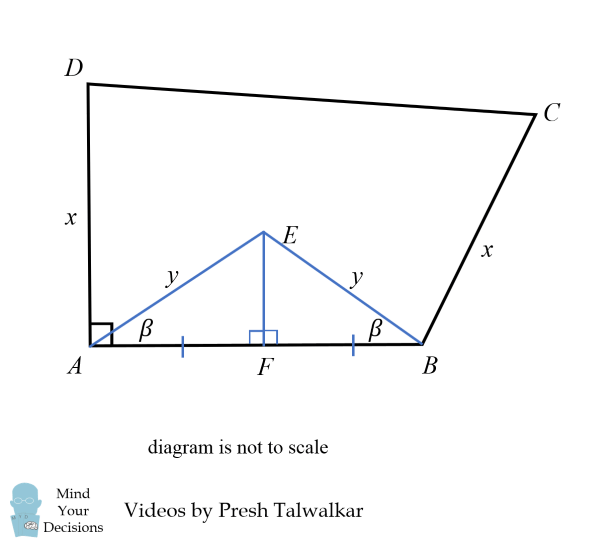
Từ đó, ta có:

góc FAE + góc DAE = góc FBE + góc CBE = α + β => góc DAB = góc CBA => α + β = 90° = 100° => 90 = 100.

Tìm lỗi sai trong cách chứng minh trên.